Clicca per ZOOM

Progettazione e Realizzazione Meridiane e Orologi Solari

Bartolini Simone - Gnomonista in Firenze

AN OUTLINE OF SPHERICAL ASTRONOMY

The Celestial Sphere and the Local Reference Systems
 
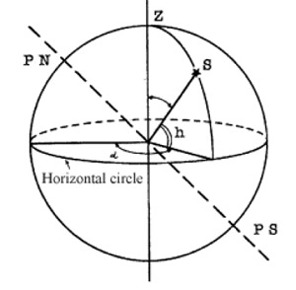
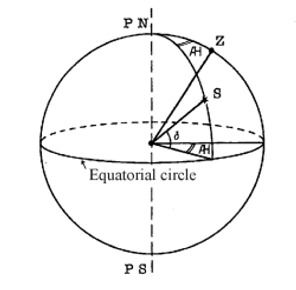
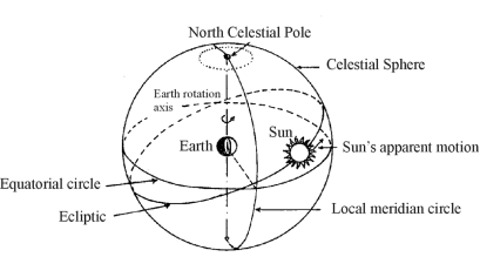
We define the Celestial Sphere as an ideal sphere (imagining its centre coincident with the geocenter and its radius infinite), on which the apparent positions of the stars can be represented together with the North Celestial Pole and the South Celestial Pole, as the intersections of the Earth's rotation axis with the Celestial Sphere.
Among the other fundamental elements which can be represented on the Celestial Sphere are: the Equatorial circle, as the intersection with the terrestrial equatorial plane, and the Meridian circles, as the intersections with the planes containing the Earth's rotation (or polar) axis. The position of the terrestrial observer can be represented as well on the Celestial Sphere, as the intersection with his vertical (or plumb) line, and is called the Zenith of the observer.
The position of every point on the Celestial Sphere - and hence of a star whatever, including our Sun - can be defined resorting, e.g., to a couple of local coordinates. The two main Local Reference Systems for those coordinates are: the Alt-Azimuth System and the (so-called) Hour System.
 
›
 The Alt-Azimuth System bases on the Horizontal circle on the Celestial Sphere, which is the intersection with the local horizontal plane, and on the Meridian circle of the observer (containing the North Celestial Pole and the Zenith). The angular distance (h) from the Horizontal circle to the star position is the Altitude; the other coordinate is the Azimuth (α), which is the angle (counted clockwise in degree, minutes and seconds) between the above Meridian circle (containing the geographic north direction) and the Meridian circle of the star (see Pic.1).
 
 
 
 
 
 
 
   
›

The Hour System bases on the Equatorial circle and on the Meridian circle passing through the Zenith's observer, taken as the other reference circle. The Hour angle of a star is then defined as the angle (H), counted clockwise in hours, minutes and seconds, between the observer's Meridian circle and the Meridian circle of the star. The other coordinate of the star, the declination, is the distance angle (δ) of the star from the Equatorial circle: this angular distance - of course applicable also to the Sun - is counted in degree, primes and seconds, positively north wise and negatively south wise. It can be considered the analogue, on the Celestial Sphere, of the (terrestrial) Latitude (see Pic.2).
 
 
 
 
 
 
 
 
 

 
   
Pic.1
Pic.2
 
The Sidereal Day and the Apparent Solar Day
 
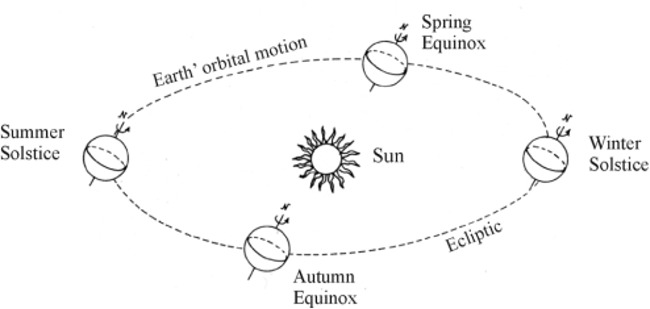
As well known, the Earth spins around its Polar axis at an almost regular rotation rate. That permits to define the Sidereal day as the time interval between two successive passages of a star on the same Meridian (which can be, e.g., the Greenwich reference Meridian or even the observer's Meridian). Moreover, the Earth revolves around the Sun along a path whose image on the Celestial Sphere is called the Ecliptic; the time period of revolution is called the Tropical year (Pic.3).
 
 
Pic.3
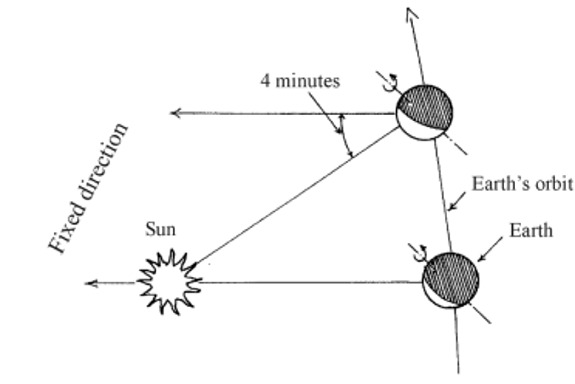
Of course, during a complete rotation the Earth covers also a part of its orbit around the Sun, so an observer on the Earth who could hypothetically "see" both the Sun and a distant (fixed) star on his Meridian at the same time, after a complete Earth's rotation would see the same star again on his Meridian (by definition!), but the Sun a little bit behind (or late) with respect to his Meridian (see Fig.4). After a further small amount of time also the Sun will reach the observer's Meridian, thus
completing its own period, which is called the Apparent 1 solar day.
 
 
 
Pic.4
 
1 Note that the adjective "apparent" here means that one makes reference to a "real" celestial object, as opposed, e.g., to the
adjective "mean" referring to a fictitious (conventional) point on the Celestial sphere, such as the mean Sun.
 
If we assign to the Earth rotation period the value of 24 sidereal hours ( = 1 Sidereal day) and to the time interval between two successive passages of the Sun on the same observer's Meridian (culminations) the value of 24 apparent solar hours ( = 1 Apparent solar day), it can be observed that one Sidereal day corresponds to about 23h56m of an Apparent solar day. So it turns out that the latter is about 4 minutes longer (in terms of Apparent solar time!) than the former.
Finally, the Local sidereal time and the Local apparent solar time can be defined as, respectively, the hour angle of a specific point on the Celestial Sphere (the Equinox γ, or Vernal point, at rest with respect to the fixed stars, defined as the intersection, from south to north, of the Ecliptic with the Equatorial Circle) and the hour angle of the (apparent) Sun + 12h (this convention aims to put the beginning of a solar day at midnight rather than at noon). Note that both the definitions refer to the (local) meridian of the observer. In case that the observer is on the Greenwich meridian, one speaks of Greenwich sidereal time and Greenwich apparent solar time.
As well known, the Earth's orbit is slightly elliptical: as a consequence, the distance of the Earth from the Sun is not constant, so also the velocity of the Earth along its orbit is not constant (according to the second Kepler Law). That causes a different duration of the apparent solar day depending on the period of the year: such duration may differ up to 30 seconds with respect to the mean value of the solar day (computed on an yearly basis). The accumulated differences between the Apparent solar time and the above mean value (to be defined more rigorously in the next section) sum up to values running from + 14 to - 16 minutes approximately.
For similar reasons, one speaks of Local noon instead of 12.00 hours because the noon is by definition the time of culmination of the Sun (for the local observer), which divides in two equal parts the time interval from sunrise to sunset: just at this time the Sun is exactly south of the observer, i.e., on the local meridian. On the other hand, very rarely the Local noon corresponds, e.g., to 12.00 hours of our clocks (due to the use of the hour zone and to the already mentioned difference between Apparent and Mean solar time).
 
The Mean Solar Day and the Mean Solar Time
As pointed out before, the Mean Solar Day is the mean of the Apparent Solar Days over the period of one year: it can be imagined as generated by a Fictitious Mean Sun moving uniformly on the Equatorial Circle and coinciding with the Apparent (or true) Sun at the intersection points of the Equatorial Circle with the Ecliptic (remember that one of these is the Equinox γ).
In this way, one obtains a uniform measure of time - still maintaining a conceptual connection both to the Earth rotation and to the Sun position - resulting from the daily passages of the Fictitious Mean Sun over a Meridian at constant time intervals (24 hours), i.e., the Mean Solar Day.
The Local Mean Solar Time can be defined as the hour angle of the Fictitious Mean Sun + 12h; in particular, the Greenwich Mean Solar Time (or GMT) is equal to 12h + hour angle of the Fictitious Mean Sun on the Greenwich Meridian and is called Universal Time (UT).
 
 
The Equation of Time
 
The spread usage of the clocks, as time keeping devices running necessarily at a uniform rate (on account of the Newtonian conception of time homogeneity), made quite natural the adoption of the Mean Solar Time for the civilian purposes. As a consequence, it was necessary to establish a link to the Apparent Solar Time (typical, e.g., of the "solar" clocks, such as the sundials): this connection is known as the Equation of Time and is simply the difference between the Local Mean Solar Time (tm) and the Local Apparent Solar Time (ta):
 
Equation of Time = tm - ta
 
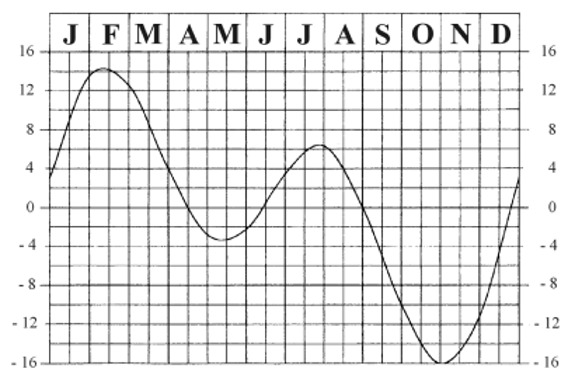
According to that definition, the (apparent) midday coincides with the (mean) midday just four times in a year: two times (14th June and 1rst September) due to the very definition of Local Mean Solar Time which prescribes the equality of the two types of time at the intersection points of the Equatorial Circle with the Ecliptic; the other two times (15th April and 25th December) for symmetry.
In the other times of the year the apparent midday sometime is early and sometime is late with respect to the mean midday (the value of the Equation of time is slightly different also depending on the year, and can be found in the Ephemerides and Astronomic Almanacs). The Table below reports the values of the Equation of time, expressed in minutes.
 
 
Pic.5
 
Moreover, the Equation of time finds a pictorial description through a "eight-shaped" curve (mathematically, a lemniscate), which is commonly drawn on the sundial's face and permits to graphically read the Local Mean Solar Time by the position of the shadow of the gnomon on the curve (it would be virtually possible to draw a lemniscate for each hour line on the sundial). In other words, it represents, on the sundial's face, the successive positions occupied by the Sun on the Celestial Sphere, at the same time of each day, during one year. The following picture, made up by photographs, taken from the same position, at the same hour and at 9-10 days intervals, is an impressive example.
 
 
The Hour Zone
For practical reasons, the Earth surface has been divided into 24 zones, called Hour Zones, each comprised between two meridians separated by an amplitude of 15 degree, corresponding to one hour. All the territory included in a single hour zone is conventionally given the same hour (namely, the hour of central meridian of the zone).
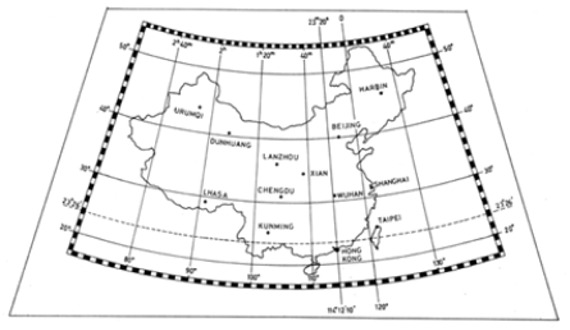
The territories of some Countries cover more than hour zone. In particular, the territory of China is included in about four hour zones; however, the "official" hour in China is just one and conventionally is relevant to the hour zone with the central Meridian 120° East from Greenwich (as a consequence, when the Sun passes over that central Meridian at midday of any day, the Earth must perform a further rotation to pass over the Hong Kong Meridian; the value of that rotation is equal to the longitude difference between the central Meridian and the Hong Kong Meridian, which is 5°47'50" , corresponding to 23m11s in time units); (see Pic.6).
 
 
Pic.6
 
The Equinoxes (or luni-solar) precession
 
On repeating the determination of the coordinates of the stars after some years, one finds that such coordinates are not exactly the same: indeed, on transforming the Equatorial coordinates to Ecliptic coordinates (longitude and latitude), one sees that, while the latitudes of all the stars remain almost the same, the longitudes increase by an amount of about 50" per year. Therefore, one can deduce that the Celestial Sphere is moving uniformly, with a slow rotation around the Ecliptic poles, from West to East, with an angular velocity of 50" per year, so that a 360° turn is performed in 25765 years.
That phenomenon was observed already in the 2nd Century B.C. by Hypparchus, who, comparing his own observations with those performed two centuries before, found a difference of 2° in the longitudes of all stars.
The longitudes here are coordinates counted from the point γ (Summer Equinox) , which has been already defined as one of the intersections of the Ecliptic Circle with the Equatorial Circle. Thus the constant increase of the longitudes can be alternatively explained admitting a retrograde motion of 50" per year of such point along the Ecliptic, or by a motion of the Equator, or by a motion of both the circles. Anyway, since the latitudes of the stars remain practically the same, one concludes that the Ecliptic is practically fixed among the stars and the Equator is moving instead, or - which is the same - the polar axis.
Which are the causes of this motion?
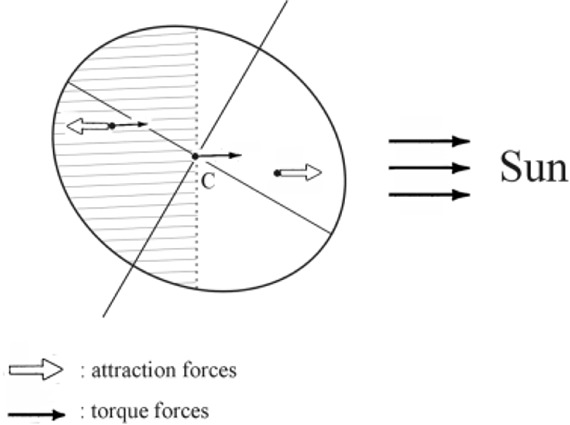
Analysing the situation of the gravitational interactions, one sees that the Sun exerts a gravitational attraction to the Earth which, if the Earth were a spherical homogeneous mass, could be considered as applied to the geocenter. Since this is not the real situation (the Earth's shape is approximately ellipsoidal and with a definite inclination of its rotation axis with respect to the ecliptic plane), we have instead to take into account the fact that the Earth's hemisphere closer to the Sun is attracted more than the one farther away (see Pic. 7). That creates a torque with respect to the baricentre (technically obtained subtracting the force acting at the baricentre - which is also the geocenter - respectively from the forces acting at the baricentres of the above hemispheres) which, tending to move the rotation axis, generates a precession motion just like it happens with a top.
 
 
Pic.7
The Sun is not the only celestial body to exert a force to the Earth: also the Moon has a similar, though minor, effect, and the motion, which results from the combination of those effects, is illustrated in Pic.9.
Among the consequences of precession, we note that today the Spring Equinox is no more coincident with the beginning of Aries Constellation: so, nowadays, it can be found in the Pisces Constellation (the one before), the Taurus sign is occupied by the Aries stars, an so on.
In any case, by convention, the diurnal lines of sundials make reference to the Zodiac as it was 2000 years ago.
Pic.8
Pic.9
 
The Seasons
 
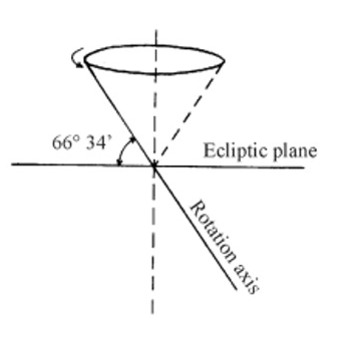
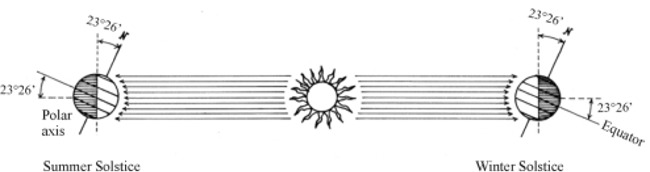
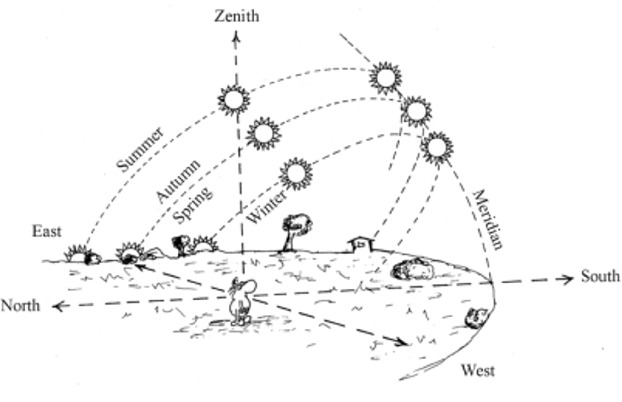
The inclination of the Earth rotation axis is about 23°26' with respect to the Earth orbital plane (the Ecliptic), and is responsible of the different duration of day and night and of the alternation of seasons; moreover, such duration is different from place to place on the Earth depending on the latitude. Only on the Equator the duration of day is equal to the duration of night, because the Equator is the only parallel of latitude which is always in shadow by exactly one half (the other half being illuminated by the Sun; see Pic.10), while the difference between day and night is more and more sensible when approaching the Poles, where it reaches its maximum (6 months in the daylight; 6 months in the night obscurity). Pic.10 clearly shows how the Northern Hemisphere (our Hemisphere) is more illuminated than the Southern Hemisphere during the Summer time; the opposite situation occurs during the Winter time. This longer illumination is possible just because the Sun has a larger amplitude, i.e., it rises before (in the north-east direction) and goes down after (in the north-west direction), during the Summer time, with respect to the Equinoxes. During the Winter time, instead, the relevant shorter illumination is possible because the Sun rises in the south-east direction and goes down in the south-west direction, running on a shorter path in the sky (see Pic. 11).
 
 
Pic.10
 
 
Pic.11
 
During one year, at midday hour, the altitude of the Sun is not always the same and will reach its maximum and minimum values at the following dates:
 
Summer Solstice (June 21): Sun altitude = 90° - latitude of the place + 23°26'
Winter Solstice (December 21): Sun altitude = 90° - latitude of the place - 23°26'
In the two intermediate times, when the Sun is on the Equatorial circle, we have:
Spring Equinox (March 21): Sun altitude = 90° - latitude
Autumn Equinox (September 23): Sun altitude = 90° - latitude
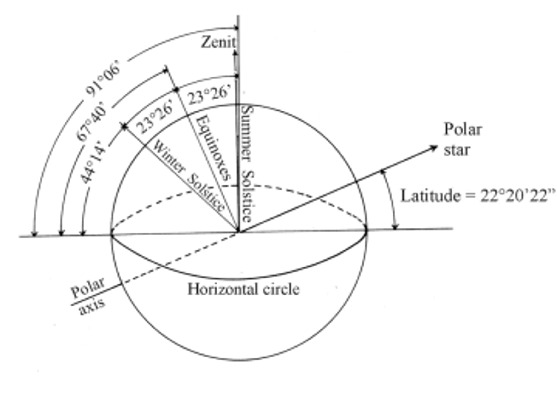
The Hong Kong latitude is about 22°20'22", so we will have, at midday hour, the following Sun altitudes: Equinoxes = 67°39'38", Summer solstice = 91°05'38", Winter solstice = 44°13'38" (Pic.12).
 
 
Pic. 12
 

 

 
 
     
||